Geog 337: Final Project

Mapping the Interaction Between Groundwater and the Surface Water Body of White Bear Lake, Minnesota

Melissa Hackenmueller 

Introduction

            White Bear Lake saw record lows in 2012 and 2013, which lead the concerned community members to sue the Minnesota Department of Natural Resources on the claim that they had poorly managed the groundwater withdrawals in the region; therefore, causing the significant decline in the lake level. This lead me to the question, could the groundwater levels be mapped throughout this region using ArcGIS and would these water table maps also show the same pattern as the surface water? The goals of my project entailed creating temporal water table maps of the region, comparing these maps to each other, and then to the water levels of White Bear Lake.

            White Bear Lake is located in Ramsey and Washington counties, which are located in east-central Minnesota. My study area encompasses a 12 km radius around the lake (Figure 1). The lake is underlaid by a glacial sediment aquifer and then a series of bedrock sandstones (Figure 2). White Bear lake is a city of about 24,000 people and is located NE of Minneapolis, Minnesota (U.S. Census, 2010).

Figure 1. Yellow circle in the east-central portion of
Minnesota is the extent of my study area.

Figure 2. A cross-section showing the series of
unconfined aquifers that lie beneath White Bear Lake.

            The data for this project all came from two branches of the Minnesota state government. I found the Minnesota counties shapefile, the roadways shapefile, and the surface water features shapefile from the Geospatial Information Office. I found the White Bear Lake Water Levels (Figure 3) and the monitoring well data from the Department of Natural Resources.

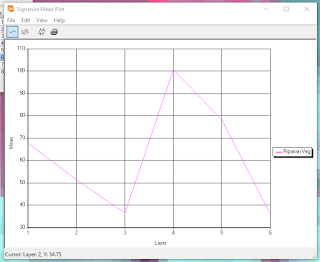
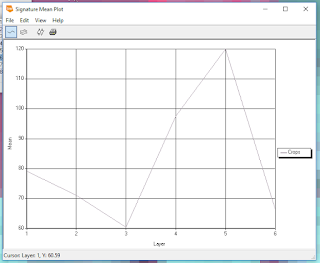
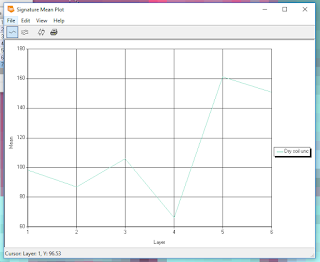
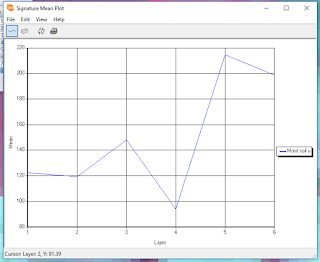
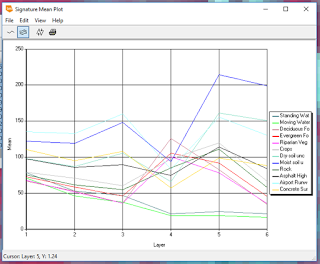
Figure 3. This graph shows the water level variations
 in White Bear Lake since the late 1960s. 

Methods

            The first step in this project was to use the select by attribute tool to narrow down my data sets to my study area. Next, I used the proximity > buffer tool to create a 12 km radius around White Bear Lake to map the extent of my study area (Figure 4). The last step of pre-processing was to digitize the monitoring wells within the study area. Since my goal was to look at the temporal change of the water table I digitized the wells for 1978, 1986, 1998, 2007, and 2017. Another goal was to determine if the groundwater followed the same pattern of highs and lows as the surface water, so I chose two major highs and two major lows in the record and digitized wells for those times too. As seen in Figure 3 above, White Bear Lake had a major high in 1986 followed by a major low in 1991 and a major high in 2003 followed by a major low in 2013. These are the years that I choose to digitize wells for.

Figure 4. This map shows the 12 km buffer that I created around
White Bear Lake to show the extent of my groundwater study area.

            The major and most important method of this project was to interpolate between the digitized well location to create a water table map for the entire study area. I used the inverse distance weighted (IDW) tool to perform this interpolation. I used IDW eight separate times in order to get water table maps over time and to map the highs and lows determined above. Before I analyzed the interpolation maps, I made sure that all of the ranges of water table levels were homogeneous to ensure that they could be compared and contrasted easily and accurately.

Results and Analysis

            Figure 5 is all of the interpolated water table maps. Overall, the water table maps throughout the 50 years didn’t change dramatically at all. The first thing I noticed during analysis was that the water table became lower as you moved to the SW. Within 1986 and 1998 the water table also became lower to the NE. The highest water table levels were consistently to the North with the center of my study area always having relatively average water table levels for the region. The interpolation becomes more complicated as you move through time, which is probably due to higher concentration of wells. In 2007 there is a very low spot in the NW corner of White Bear Lake, I believe this may be an out liar or mis-reading of some sort, as it doesn’t fit the other well readings in that area. Overall, through time the water table doesn’t change very much.

Figure 5. This series of maps shows the progression of the water table through time. The top, left map is
the earliest (1979) and the bottom, middle map is the most recent (2017). The light blue represents a high
water table (close to the ground surface) and the dark blue represents a deeper water table. 

            I then took a look at the water table maps I made during the highs and lows record on White Bear Lake (Figure 6 and Figure 7). When comparing the high of 1986 and the low of 1991, nothing stands out in correspondence to the 6 foot drop in surface water. There is slightly higher peaks in 1986, but nothing dramatic that represents the significant changes in surface water. I then took a look at the 2003 high and the 2013 low, to see if this had some difference. To my surprise, the water table maps looked very more similar. There is a low shown in the NW portion of White Bear lake in the 2013 water table map but this low is also shown in the 2003 water table map. The dramatic surface water changes, didn’t seem to be represented in the water table maps that I have created.

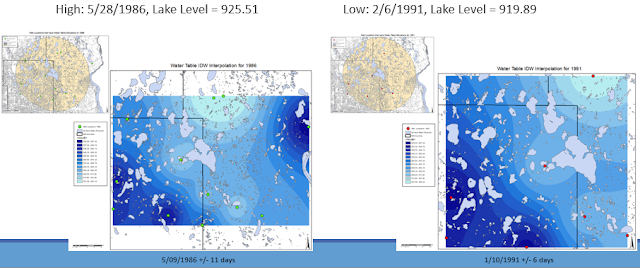Figure 6. These maps compare a time of high and low surface water levels with the corresponding
groundwater levels. The left is the high time of 1986 and the right is the low period of 1991.

Figure 7. These maps also compare a time of high and then low surface water levels. These are a more
 recent set of highs and lows. The left is a lake level high in 2003 and the right is a lake level low in 2013.

Conclusions

            Overall, the water table maps that I created using IDW interpolation didn’t accurately represent the water table in real life. I came to this conclusion because of the little variations in the groundwater in reflectance to the large variations within the surface water levels. Groundwater and surface water are very closely related to one another; therefore, a much closer relationship is expected. My future work would include a more dense amount of wells in my study area to create a more accurate water table map. I could also quantify the groundwater pumping in the area to determine the cone of depression that is interacting with White Bear Lake. Also, incorporating precipitation into the equation would allow for a much more comprehension evaluation of the causes of decline in White Bear Lake. 

Data Sources

Minnesota Department of Natural Resources. GIS Shapefiles. State of Minnesota.

Minnesota Geospatial Information Office. GIS Shapefiles. State of Minnesota.

U.S. Census, 2010.

Literature Review References

Kalivas, D. P., Kollias, V. J., and Karantounias, G., 2003, A GIS for the assessment of the spatio-temporal changes of the Kotychi Lagoon, western Peloponnese, Greece: Water Resources Management, v. 17, no. 1, p. 19-36.

Moeckel, J., Ekman, J., 2016, Findings of Face and Order White Bear Lake Protective Elevation White Bear Lake, Ramsey and Washington Counties, Minnesota Department of Natural Resources.

Neto, R. T. D., Santos, C. A. G., Mulligan, K., and Barbato, L., 2016, Spatial and temporal water-level variations in the Texas portion of the Ogallala Aquifer: Natural Hazards, v. 80, no. 1, p. 351-365.

Geog 338: Lab 8

Spectral Signature Analysis and Resource Monitoring

Melissa Hackenmueller

Background and Goals

            The main goal of this lab is to become more familiar with and gain hands on experience with the measurement and interpretation of spectral reflectance signatures. Part one of this lab will teach how to collect spectral signatures from satellite imagery, graph these signatures, and then analysis them. The second portion of the lab will be learning how to use Erdas Imagine to monitor the health of vegetation and soils using simple band ratio techniques. This will include mapping the findings using ArcMap.

Methodology

Part 1: Spectral Signature Analysis

            I used a Landsat ETM+ image of Eau Claire and Chippewa counties, Wisconsin, to analysis the spectral signatures of 12 natural and man-made features. I first loaded the eau_claire_2000.img into Erdas Imagine. I then zoomed into a water feature called Lake Wissota to collect my first spectral signature. By using the polygon tool from the drawing tab, I digitized a small polygon within Lake Wissota. Then from the raster tools I selected supervised and then signature editor. The signature editor dialog is now open. I then created a new signature form AOI, which added a new row in the dialog box. I then changed the signature name to standing water, to ensure I would remember what each new signature represented. I then clicked on the display mean plot window tool to display the plot of the spectral signature (Figure 1). I then followed the same process above with moving water, deciduous forest, evergreen forest, riparian vegetation, crops, dry soil, moist soil, rock, asphalt highway, airport runway, and a concrete surface. These spectral signatures are Figures 2-12 respectively. After all of these signatures were completed I displayed them all on one chart using the switch between single and multiple signature mode in the signature editor dialog (Figure 13).

Part 2: Resource Monitoring

            Part two was divided into two parts. The first of which is creating a vegetation health monitoring map using simple band ratio in Erdas Imagine by implementing the normalized difference vegetation index (NDVI). I used the image ec_cpw_2000 for my analysis, this covers Eau Claire and Chippewa counties. I started by imputing my image into Erdas Imagine and then using the raster tool NDVI in the unsupervised category to perform this task. Once the Indices dialog was open I saved the image into the appropriate folder and made sure the sensor was set to Landsat 7 Multispectral, the function as NDVI, and then hit run. I then uploaded the new image into ArcMap and adjusted the symbology to create a map displaying the abundance of vegetation in Eau Claire and Chippewa counties, Wisconsin (Figure 14).

            The second section of this lab was mapping the soil health of Eau Claire and Chippewa counties. I did this by performing a band ratio using the ferrous mineral ratio on the image ec_cpw_2000. Once the image was uploaded in Erdas Imagine, I used the Unsupervised raster tool of Indices. In the Indices interface I made sure to save the new image into an appropriate folder, change the sensor to Landsat 7 Multispectral, set the function to Ferrous Minerals, and hit run. Again, I uploaded the new image to ArcMap and created a map to display the spatial distribution of ferrous minerals within Eau Claire and Chippewas counties, Wisconsin (Figure 15).

Results

Figure 1. Spectral signature of standing water.

Figure 2. Spectral signature of moving water.

Figure 3. Spectral signature of deciduous forest.

Figure 4. Spectral signature of evergreen forest.

Figure 5. Spectral signature of riparian vegetation.

Figure 6. Spectral signature of crops.

Figure 7. Spectral signature of dry soil. 

Figure 8. Spectral signature of moist soil. 

Figure 9. Spectral signature of rock. 

Figure 10. Spectral signature of asphalt highway. 

Figure 11. Spectral signature of an airport runway.

Figure 12. Spectral signature of a concrete surface.

Figure 13. All of the above spectral signatures together. As I analyzed this Figure, I noticed many similarities between various signatures. The spectral signatures of standing and moving water are very similar, which is expected due to the fact that the only changing factor is the velocity of the water. The next similar cluster is the vegetation signatures (evergreen forest, deciduous forest, and riparian vegetation). I also expected these to be similar because all plants need to absorb the visible to produce chlorophyll and reflect the NIR in order to avoid damage. The moist and dry soils were also similar, which the exception of the peak in the moist soil in the MIR.

Figure 14.

Figure 15.

References

Satellite image is from Earth Resources Observation and Science Center, United States Geological Survey.

Geog 338: Lab 7

Lab 7: Photogrammetry 

Melissa Hackenmueller

Goals and Background

            The overall goal of this lab was to develop the skills needed to perform photogrammetric tasks on aerial photographs and satellite images. The goals were further separated into three parts. The goal of the first part of this lab was to ensure my understanding of photographic scales, measurement of areas and perimeters of features on an image, and calculation of relief displacement. The second portion of this lab was to increase my knowledge of stereoscopy and its uses. The last goal of this lab was to perform orthorectification on satellite images.

Methodology

Part 1

The first section of part one was designed to improve the calculation of photographic scales. The first step was to determine the distance between A and B on an image (Eau_Claire_West-se.jpg) which I measured as 2.7 inches (see figure below).

The Actual distance between the two points was measured with an engineer’s chain to be 8,822.47 feet. The following math was done and the result was a scale of 1: 39,210.98 for the image.

Actual distance: 8822.47 ft.

Photo: 2.7 inches

8822.47 ft x 12 = 105,869.6 in

2.7 in / 105,869.6 in                            divide numerator and denominator by 2.7

Scale is 1:39,210.98

The next question was also to find a photographic scale, but using the equation S= f /H –h this time. The following calculations were done to determine the scale to be 1:38,519.

            F = 152 mm /10/100 = 0.152 m *3.28 = 0.49856 ft

            H = 20,000 ft amsl

            h = 796 ft

            S = 0.49856 ft / (20,000 ft – 796 ft)   divide numerator and denominator by 0.49856 ft

            Scale is 1:38,519

The goal of the next section of part one was to determine the area and perimeter of a pond on an aerial image. Using the polygon measure tool, I carefully digitized the outline of this pond in order to get an area and perimeter (Fig. 1). The digitizing of the pond yielded an area of 37.6880 hectares and a perimeter of 4,063.42 meters. The last section of part one was calculating relief displacement of a smoke stack in an Eau Claire image (see figure below).

Tall objects are distorted in aerial photographs and the equation, d= h x r / H, is used to calculate relief displacement, which is the distance the object needed to be moved towards the principal point in order to fix the distortion. The following calculations gave a relief displacement of 0.228 inches on the smoke stack.

          H = 3,980 ft x 12 = 47,760 in

            h = 0.4 x 3,209 = 1,283.6 in

            r = 8.5 in

            d = 1283.6 in x 8.5 in / 47760 in = 0.228 in

            Relief displacement is 0.228 inches

Part 2

            The goal of part two of this lab was to generate a three dimensional image using a digital elevation model and LiDAR derived surface model. In order to accomplish this two images were needed. I imputed ec_city.img and ec_dem_2.img into Erdas Imagine. I then used the Anaglyph Terrain tool to create a stereoscopic image. The input DEM, input image, and output fields just need to be filled in and then the defaults can be used to create a new image. I then did the same processes to create a stereoscopic image with a LiDAR DSM image. 

Part 3

            The final part of this lab is orthorectification. Erdas Imagine Lecia Photogrammetric Suite will be used. The tasks of this section included creating a new project, select a horizontal reference source, collect GCPs, add a second image to the block file, collect another set of GCPs, perform automatic tie point collection, triangulate the images, orthorectify the images, view the orthoimages, and save the block file. I started by opening IMAGINE Photogrammetry in the toolbox tab of Erdas Imagine. I then choose create a new block file from the project manager that is open. I saved the output image in my desired location, chose polynomial-based pushbroom for geometric model, selected SPOT Pushbroom, and then hit okay to finish the model setup. Next, the block property setup dialog opens. I chose UTM as the projection type, Clarke 1866 as the spheroid name, NAD27(CONUS) as the datum name, 11 as the UTM Zone, North as the field, and then hit okay to conclude the set up. The next step is to add the imagery to the block. To do this I chose the add frame icon from the block project tree view, making sure that the images folder is highlighted beforehand. The image file name dialog is now open and I added the image Spot_pan.img. I next went to the SPOT pushbroom frame editor to ensure that the parameters that I inputted earlier were correct, they were so I exited.

The next step is to start adding GCPs by clicking the start point measurement tool and using the classic tool. Next, I clicked the reset horizontal reference source icon to open the GCP reference source dialog. Choose the image layer button then move on to the reference image layer dialog and imput the image xs_ortho.img. I then choose use viewer as reference so the xs_ortho image displayed on the left and the original image on the right (see Fig. below).

To begin adding GCPs, I clicked add button in the point measurement tools and then the create point icon. I clicked on the road intersection desired on the reference image (xs_ortho.img) to input my first GCP. Once, I was happy with the first point, I added the point to the same spot on the original image (spot_pan.img). The first GCP was successfully added, so I followed the same procedure above for the next 8 GCPs. I then saved my work because the last two GCPs will be added from a different reference image. To add a new reference image click on the reset horizontal reference source icon again, this time I chose NAPP_2m_ortho.img as my reference. I added two more GCPs with this new reference image following the same structure as above. Now, a vertical reference source can be used to collect elevation information, I used the palm_springs_dem.img. I choose the reset vertical reference source icon this time and inputted the desired reference image. Once, the image was inputting I selected all of my Point # column and clicked on the update Z values of selected points icon, which updated the Z values based on the palm_springs_dem.img. The Figure below is what my X, Y, and Z reference columns now look like.

            The next section of this lab focuses on the set up before collecting tie points. First, the type and usage columns need to be filled out. I selected the type column and then choose formula from the column options. Here, I typed in “Full” and then hit apply. I repeated the steps above for the usage column, but typed “control” this time. Now that these columns are updated, I hit save and closed the point measurement tool. Next, I moved to the editing of the spot_panb.img by clicking the add frame icon and adding the image. I then highlighted row #2 and clicked the frame properties icon. The SPOT pushbroom frame editor opens, I hit okay to accept the parameters. Next, I used the point measurement tool to located the points that have already been collected from the first image, spot_pan, and plot them in the second image, spot_panb. I made sure to highlight point #1, before using the create point icon to add the points to the spot_panb image. Some of the points were not located on spot_panb.img, but I added all the similar points following the same procedure as above and then saved. My images now look like Figure 2.

            The next step is tie point collection, triangulation, and ortho resampling. From the point measurement tool palette I chose the automatic tie point generation properties icon. Then I used all available for image used, exterior/Header/GCP for initial type, set the image layer used for computation to 1, set the intended number of points/image field to 40, and hit run. This automatically set points tied to both images, my points now totaled 37. After I checked the accuracy of the points created, I saved them. Now, that all the tie points are found I can perform triangulation. On the IMAGINE photogrammetry project manager, I chose the Triangulation properties. I put the iterations with relaxation value to 3, the image coordinate units for report to pixels, the type of point to same weighted value, the x, y, z values to 15, then ran the triangulation, and saved it in an appropriate spot. I started the final process of ortho resampling by clicking on the ortho resampling process icon. I selected DEM as the source, inputted the palm_springs_dem.img, entered the output cell size to 10 for both x and y, saved the output file in an appropriate spot, ensured that the resampling method was bilinear interpolation, made sure to add both spot_pan.img and spot_panb.img, and then I hit okay to start the resampling process. Finally, I created a ortho resampled image (Figure 3).

Results

 

Figure 1. This image shows the points that I collected around the pond
in Eau Claire using the measurement tool to get an area and a perimeter.

Figure 2. This image shows the GCP points that I collected on
the spot_pan.img and then on the spot_panb.img.

Figure 3. This is my final image output after the process of ortho
resampling on both the spot_pan.img and spot_panb.img.

References

Digital Elevation Model (DEM) for Eau Claire, WI is from United States Department of Agriculture Natural Resources Conservation Service, 2010.

Digital elevation model (DEM) for Palm Spring, CA is from Erdas Imagine, 2009.

Lidar-derived surface model (DSM) for sections of Eau Claire and Chippewa are from Eau Claire County and Chippewa County governments respectively.

National Aerial Photography Program (NAPP) 2 meter images are from Erdas Imagine, 2009.

National Agriculture Imagery Program (NAIP) images are from United States Department of   Agriculture, 2005.

Spot satellite images are from Erdas Imagine, 2009.

Geog 337: Lab 3

Lab 3: Building a Geodatabase

Melissa Hackenmueller

Purpose and Background

The purpose of this geodatabase is to organize my final project data. The user of this geodatabase will be only me because it is for a course project. I chose a file geodatabase, because of the larger storage space that it has compared to a personal geodatabase. The extent of my geodatabase is the state of Minnesota. The largest my final map will be is about 1:400,000 (tri-county area around White Bear lake) and the closest extent about 1:50,000 (just White Bear Lake). The projection of the geodatabase is NAD_1983_UTM_Zone_15N. I didn’t incorporate topology or annotations to my geodatabase, because neither are necessary for the organization of my project. My project doesn’t include integrated road systems, where topology is required. My project doesn’t need extensive labeling so annotations are not needed. All of my data is from various government sources, so all has extensive metadata included. I don’t plan on expanding this metadata for my project because my work will not be used in future work as it is for a course project.

Geodatabase Organization

Feature Datasets

            I created two feature datasets within my geodatabase. The first called Hydro_Features. This dataset includes three feature classes. They are Lake_Bathmetry, Lakes_and_Ponds, and White_Bear_lake. The data inside of the Lake_Bathmetry feature class is lake contours for a majority of Minnesota lakes. The attribute fields include depth, absolute depth, lake name, and shape length. The Lakes_and_Ponds features class includes all lakes and ponds polygons in Minnesota. The attributes of this feature class include DNR identification numbers, acres, shore mileage, city name, shape length, and shape area. The last feature class in the Hydro_Features dataset in the White_Bear_Lake feature class. This includes the same attributes and the Lakes_and_Ponds feature class.

            The next feature dataset I created is called MN_Counties. This includes the MN_CountiesOfInterest feature class. The MN_CountiesOfInterest feature class includes the counties surrounding White Bear Lake. The attributes includes the county code, county name, another identification code, shape area, and shape length.

Features Classes

I included two feature classes within my Final_Project geodatabase. These two feature classes are MN_Aquifers and Well_Locations. MN_Aquifers are polygons that represent the top aquifer of that region. The attributes include area, perimeter, bedrock hydrogeology code, and bedrock hydrogeology key. The Well_Location feature class is a point feature class that shows the location of all wells in the state of Minnesota. The attributes in this feature class include the county code, the location in township and range, the elevation of the site, the drill depth, drill date, other drill information, and aquifer the well is drilled in. I also included a table into my geodatabase called White_Bear_Lake_WaterLevel. This table included water level data of the lake since the 1920’s and is essential to the completion of my project.

Behavior Settings

The behavior settings that my geodatabase includes are the default values of the feature database and feature classes. The default XY tolerance used for my feature datasets is 0.001 meters, the Z tolerance is 0.001, and the M tolerance is 0.001. The default XY tolerance that I used for my feature classes is 0.001 meters. I didn’t use any other behavior settings because I didn’t feel that subtypes or domains were needed for my project, as I will not be adding excess information to my feature classes.

Conclusion

The geodatabase that I have created for this final course project is a simplistic way to organize the data and the results that I have compiled. It is composed of two features datasets that contain feature classes within them, two stand-alone feature classes, and a table. It contains no topology or annotations and has minimal behavior settings, but it is fitting for the project that I am conducting.

GEOG 338: Lab 6

Lab 6: Geometric Correction

Melissa Hackenmueller

Background

Lab six was designed to introduce students to geometric correction. Geometric correction is very important in image pre-processing for it needs to be used to accurately extract biophysical and sociocultural information. Two types of geometric corrections will be performed in this lab. The first is image-to-map rectification and the second is image-to-image rectification.

Methodology

            The first section of this lab uses a USGS 7.5 minute digital raster graphic image of the Chicago Metropolitan Area and a corrected Landsat TM image of the same area. The first step is to input both the Chicago_drg.img and the Chicago_2000.img into Erdas Imagine. Next, I clicked on the control points tool of the multispectral toolbox. A select geometric model dialog will open. I selected polynomial, then image layer, added my reference map (Chicago_drg.img), and then hit okay one last time in the reference map information dialog. This then will bring up a multipoint geometric correction window. This window showed my input image (Chicago_2000.img) on the left and my reference image (Chicago_drg.img) on the right. Ground control points could now be added to my maps, but I first made sure that any existing ground control points were deleted. Then I used the create ground control points tool to input a point on each map in the same area. I then repeated this process three more times to get four ground control points that were evenly distributed across my images. Once, this was done I looked at my total RMS error and it was very high. To decrease the RMS error, I zoomed into each ground control point and adjusted it to accurately represent the area on the other image. Once my RMS error was below 2 I decided that my image was spatially correct enough for this project (Figure 1). Ideally the RMS error should be below 0.5 for the geometric correction to be accepted in the remote sensing field. I was content with my RMS error so I used the display resample dialog button to create a rectified, geometrically correct image.

            Part two of this lab was to use image-to-image rectification to create a geometrically correct image of the east side of the Sierra Leaone. I started by importing the sierra_leone_east1991.img and the sl_reference_image.img into two separate viewers in Erdas Imagine. I then chose control points from the multispectral toolbar. In the geometric model window I selected polynomial, then image layer, imported my reference map (sl_reference_image.img), accepted the default inputs for the reference map information, and finally chose 3^rd order polynomial. I then clicked on the create ground control points tool and started to add my points as I did in part one. This time I added 12 ground control points to my image. Only 10 are needed for 3^rd order polynomial, but a few extra points allow the rectification to be more accurate. Once I placed all my ground control points, I more accurately placed them until my RMS error was below 1 (0.5 would be ideal, but was not necessary for this lab). Figure 2 is an image of my RMS error. I was content with my RMS error so I used the display resample image dialog button to create a geometrically correct image (sl_east_gcc.img). This image could then be used to more accurately analysis the area of interest.

Results

Figure 1: This image displays the ground control points that I used for my image-to-map rectification.
The ground control points are distributed evenly about the image to provide an accurate output image.
My RMS error is below 2, which was the goal for part one of this lab.

Figure 2: This image displays my ground control points for my image-to-image rectification. 

The RMS error is below 1 as that was the goal for part two of this lab. 

References

Satellite images are from Earth Resources Observation and Science Center, United States Geological Survey.

Digital raster graphic (DRG) is from Illinois Geospatial Data Clearing House.

GEOG 338: Lab 5

Lab 5: Lidar Remote Sensing
Melissa Hackenmueller

Goals & Background

            The primary objective of Lab 5 was to learn the basics of lidar data structure and processing. In order to obtain these goals, the lab was separated into three parts. The first of which was an introduction to point cloud visualization in Erdas Imagine in comparison to ArcMap. The second portion of this lab was created to learn how to generate a LAS dataset and gain experience with lidar point clouds on ArcGIS. The last section of this lab was designed to give students an introduction to the generation of lidar derivative products (DSM, DTM, and intensity images).

Methodology

            Part one of this lab uses Erdas Imagine and ArcMap to display lidar point cloud data. The first step I conducted was selecting all the LAS files of interest into Erdas Imagine. Next, I opened the tile index file QuarterSections_1.shp into ArcMap to locate my LAS data in Erdas Imagine. In doing this, I learned that ArcMap is much easier to analysis lidar point cloud data from than Erdas Imagine. Therefore, part two and three will be mainly using ArcGIS systems instead of Erdas Imagine.

            The objective of part two was to generate a LAS dataset and then explore the data within ArcMap. The first step was to add a new LAS dataset in ArcMap; I named mine Eau_Claire_City to give a description of what the study area is about. Next, I went to the LAS Dataset Properties of my newly made dataset and added all the LAS files needed from my project. After this I went to the statistics tab of the properties and hit calculate to produce statistics for the data I just imported. Statistics for the entire dataset will populate and statistics for individual files can be found on the LAS file tab. I then used these statistics to do a QA/QC check by comparing my minimum Z and maximum Z values with the known elevation of my study area, in this case, Eau Claire. The next step is to add coordinate systems to your dataset. After consulting the metadata, I determined that the NAD 1983 HARN Wisconsin CRS Eau Claire (US Feet) projection was the best fit for my XY coordinate system. I learned from the metadata that the NAVD 1988 US feet projection should be used for the vertical coordinate system of this data. This then concluded the editing of the new dataset, so I added the Eau_Claire_City.lasd into ArcMap to display it. I then added a shapefile of Eau Claire county to confirm that my dataset was properly located; it was and so I then removed the county shapefile (Figure 1). Next, I zoomed into my a small portion of my dataset to analyze my point cloud data (to save time the data doesn’t load the point cloud data at full extent). Once, zoomed in your data should appear, similar to Figure 2. Next, I used the LAS Dataset toolbar to examine the aspect, slope, and contours of my dataset. Another tool I utilized on the LAS Dataset toolbar was the profile view tool, this allows you to draw over a portion of interest on the map and then display a cross-sectional view of the point cloud data. This data can be viewed in 2D and 3D. Now, that I have my LAS dataset created in ArcMap, it is time to create products from it.

Figure 1: My LAS dataset lies correctly within the Eau Claire County shapefile confirming that the properties of my Eau_Claire_City LAS dataset were properly imputed. 

Figure 2: This shows a small portion of my point cloud dataset. The dataset must be zoomed in to in order for the point cloud data to display. 

             The objective of part three was to take the Eau_Claire_City LAS dataset and generate various lidar derivative products. First, I created a DSM using the LAS dataset to raster tool. My input was the LAS dataset and I named my output EC_FR_2m. I then chose the binning method and imputed the value field to elevation, the cell type to maximum, the void filling to Natural_Neighbor, the sampling type to Cellsize, and the Sampling Value field to 6.56168 ft (roughly 2 m). After these inputs were completed I ran the tool. To enhance the DSM that I just created I used the Hillshade tool from the 3D analyst tools. I imported the EC_FR_2m file I just created and ran the tool. Figure 3 is the hillshade DSM product that I created. My next goal was to create a DTM derivative. I made sure that my filter on the LAS Dataset toolbar was set to ground and the point tool to elevation. I then used the LAS dataset to raster tool again. I named the DTM, EC_DTM_2M and used all the same binning method parameters as before, except I chose minimum as the cell assignment type. I ran the tool creating my DTM and then I used EC_DTM_2M file to create a hillshade image. Figure 4 shows the bare earth product that I created in this step. The final derivative product that I created in this lab was a lidar intensity image. First, I set my dataset to point and the filter to first return. I then opened the LAS dataset to raster tool and imported the Eau_Claire_City dataset into the input. I imputed Intensity into the value field, Average into the binning cell assignment type, Natural_Neighbor into the void fill, 6.56168 into the cell size, and named the output EC_Int. I ran the tool and the intensity image was added to the map. The contrast of the intensity map is difficult to see in ArcMap, so I imported the EC_Int.tiff file into Erdas Imagine to enhance the contrast (Figure 5).

Results 

Figure 3: The hillshade DSM derivative product that I created from my Eau Claire City point cloud data. 

Figure 4: The hillshade DTM (bare earth) derivative product that I created from the Eau Claire City point cloud data.

Figure 5: The Intensity image that I created from the Eau Claire City lidar point cloud dataset, displayed in Erdas Imagine. 

References

Lidar point cloud and Tile Index are from Eau Claire County, 2013. 

Eau Claire County Shapefile is from Mastering ArcGIS 6th Edition data by Margaret Price, 2014.